Marcel Duchamp’s Impossible Bed and Other “Not” Readymade Objects: A Possible Route of Influence From Art To Science / Part II
Part II of Rhonda Roland Shearer’s essay
was originally published in
Art & Academe (ISSN: 1040-7812),
Vol. 10, No. 2 (Fall 1998): 76-95.
Copyright © 1997 Visual Arts Press Ltd.
Duchamp said that he was a “meticulous man”; yet he “lost” most of his original readymades, (which we can then never find as exact duplicates in stores or historical records), but he faithfully keeps the “original” photographs. In creating his Green Box Notes, (1934), Duchamp said he ran all over Paris to find the exact paper used in the originals. He even went so far as to make metal templates to recreate the note paper’s often irregular, torn edges!
Arturo Schwarz surely must have noticed, when making his series of readymade reproductions, that he could not just walk into a store and buy any of the supposedly “off the rack,” “let’s buy it, display it in a museum and enjoy the joke” objects. Shouldn’t we use our (non-retinal) minds and recognize that our perspective on the readymades has been wrong; as illustrated by the wrong perspective within the readymades. (Duchamp was involved in producing a magazine titled Rong Wrong (1917). He said that the printer got it wrong too, because he left out the first W in the magazine title. Does this magazine also form part of the same continuum of doubt — Rong [printer], Wrong [magazine], wrong [readymades], wrong [us, about the readymades]?1 After all, doubt leads us, and always occurs before any discovery? Duchamp also made an etching (1959) using only the letters, NON. Was “NON” left floating alone as an isolated clue meant to be combined with something else in his oeuvre that we thought to be true in our perspective? For example, “NON-readymade?” Duchamp himself continually surprised us by combining his work as he went along. A landscape drawing for example, Du Tignet, (1959) would later be combined with the Large Glass (1915-23) to create a new 3rd drawing Cols alités (1959) which revealed his work in a new combination. Duchamp himself proclaimed his “goal” to be “combinations that only grey matter can succeed in rendering” (Krauss, p 434). In chess, combinations are the creative patterns and strategies of the game — and so too, for discovery and logic. One event is an isolated fact; two events may have a causal relation or may be a chance coincidence; but three facts in relations or combination, usually marks a pattern and a discovery.
As in following the crumbs left by Hansel and Gretel, finding one “wrong” readymade, then another, and finally a whole series of examples of wrong readymades, sets up for us (in retrospect) a scenario of logical induction. Induction works fundamentally as a three-step “ascending” process moving from the “particular” to the “general”: step 1, we find one particular fact for example; step 2, we discover many similar facts or examples; which leads us to step 3, a generalization or a discovery of a new law, giving us a new perspective. 2 Since we now have stepped up from single facts (readymades observed to be wrong), to a set of related facts (a set of wrong readymades), we are forced to rethink our perspective and to make a new generalization (Poincaré, 1902/1952, p16). 3
Duchamp scholars have kept silent, or simply noted the contradictions, (for example, an inability to replicate the dropping of the three threads in the 3 Standard Stoppages), leading them to conclude (in other words, to make a generalization) that perhaps the contradictions embodied Duchamp’s point and constituted an end in itself (Buskirk, p 195-199). But Duchamp was a brilliant thinker and master level chess player who competed in international tournaments. Extolling the virtues of mental beauty in chess, he declared that “while all artists are not chess players all chess players are artists” (Schwarz, 1969A, p 68).
So let’s be chess players and think. If contradiction itself constituted Duchamp’s point, this result wouldn’t be analogous in any way with the strategies, moves, and patterns that, according to Duchamp, establish the mental beauty of chess. Moreover, Duchamp said that all his artistic productions were “non-retinal” like chess. Local contradictions are analogous to single chess moves or single facts. How can such a limited item be interesting to a chess player? A local move does not define the “beauty of grey matter” that Duchamp specifically describes (Schwarz, 1969A, p 68-69).
This topic of single facts leads back to what Duchamp identified as perhaps his favorite, and most important work, the 3 Standard Stoppages. After memorializing his three acts of chance by dropping three meter-length threads, and mounting them on canvases, Duchamp later made, three wooden measuring sticks based upon his result, (as shown in Illustration 16) in Part I) and then declaring them to be a new measuring system. He then put all the elements of his system in a croquet box.

Assemblage: Three threads glued to three painted canvas strips,
5 1/4 x 47 1/4 ” (13.3 x 120 cm), each mounted on a glass panel,
7 1/4 x 49 3/8 x 1/4 ” (18.4 x 125.4 x .6 cm); three wood slats,
2 1/2 x 43 x 1/8 ” (6.2 x 109.2 x .2 cm),
2 1/2 x 47 x 1/8 ” (6.1 x 119.4 x .2 cm),
2 1/2 x 43 1/4 x 1/8 ” (6.3 x 109.7 x .2 cm),
shaped along one edge to match the curves of the threads; the whole
fitted into a wood box, 11 1/8 x 50 7/8 x 9 ” (28.2 x 129.2 x 22.7 cm).
The Museum of Modern Art, New York, Katherine S. Dreier Bequest. Photograph
©1998 The Museum of Modern Art, New York.
Combining Poincaré’s probabilistic theory of discovery with the 3 Standard Stoppages (stoppages refer to invisible mending or sewing in French), we can understand what Duchamp did. With the 3 Standard Stoppages Duchamp has given us a readymade readymade for our verification (measure and experiment) of his readymades; all in a readymade croquet box! In other words, he has given us a box of tools needed to make new generalizations — the very thing that changes by chance discovery! Upon reflection, this procedure is far more valuable than if Duchamp had handed us a new, single discovery. Discoveries, as we learned from both Poincaré and Duchamp, change “every 50 years” (Tomkins, p. 18, 34, Poincaré, 1908, p. 123). Here we have the means for verifying our own discoveries — and his! 4
Remember Poincaré’s discovery theory: an idea drops into your mind as if “readymade ” (tout fait in French). Then you must measure and “experiment ” before you can be confident that you have made a discovery. If Duchamp was following Poincaré’s discovery process he would have to verify his results by measure and experiment before he could declare a discovery — exactly as Duchamp did within the 3 Standard Stoppages.5 Dropping the three meter threads clearly constitutes an experiment.
But what was Duchamp testing? He says that he made the 3 Standard Stoppages to obtain a new measuring system and to “can chance. ” If we use one of the mathematical meanings of chance, and not the vernacular definition of randomness, Duchamp’s repeated experiments in dropping threads imitates scientific method and an approach to statistical sampling. As Poincaré noted, in an empirical world replete with both irregularity and pattern, all facts or events are unique and never exactly repeated. But as a savings grace for science, and despite all these irregularities, hidden patterns can lead to a “right ” choice of facts that will reveal some sort of unity or law. Discerning the similarity across numerous facts, allows us to generalize about the series itself and nature as a whole.
In this way, creativity is a mysterious process where the right fact can nudge us to a new perspective, and lead us to see an entire system in a new way. Poincaré claims that this right “choice ” of a fact — a process that can transform a group of facts from a pile of stones to a house — is the essence of creativity and discovery. Human beings, with their limited minds and senses, can never hold all perspectives at once. Yet all possibilities still exist. Since we can only hold one perspective at a time, chosen from the mixture in our unconscious, one must, in order to be optimally creative, always try to move perspectives and continually to choose the best combinations.
Poincaré tells us that we do this unconsciously by our intuitive “sieves, ” thereby making conscious verification by measure and experiment so important! If we “read out ” perspectives from our unconscious and then merely accept them, we will likely be placed in the position of false perception that Apolinère Enameled imposed. Without critical thinking, and without verification by our conscious minds, what we see may be wrong. Even with verification by measure and experiment, any one perspective will still be incomplete, and will change (as indicated by the history of discovery). But having the best possible perspective at any one time is different from being wrong for lack of logical verification. If better choices could have been made with critical thinking, — then we clearly have not attained our best choice of perspective.
By dropping a meter thread three times, Duchamp creates a sample from a larger infinite series of events. Duchamp doesn’t have to drop threads one hundred times. From logic and experience, we can induce, from three events, what will approximately happen for the next 100 or 1,000 tries. Even though no two facts or events are exactly alike, with the right choice of facts, nature will reveal “her ” unity. Duchamp regarded three as a minimal number of events from a larger continuum needed for making a generalization. Duchamp stated that he believed “three or three million it’s … the same thing as three ” (Cabanne, p 47). He was also well aware of “generalizations ” and spoke of how the mind uses them in constructing reality (Gold, appendix 24).
Duchamp’s use of the Milky Way, dust in fluid, and gaseous molecules as three related probabilistic systems borrowed by Poincaré’s own example to illustrate the ultimate power of generalization in revealing nature. If one makes the right choice of a fact (as a specific example, he cited the probabilistic behavior of microcosmic gaseous molecules and the Kinetic Theory of Gases), then when we apply this fact to other scales (the macrocosmic Milky Way or the human scale of dust in fluid) we will find a similar, or what Poincaré called a “qualitative, ” measure or a match in appearance (Diacu, Holmes, p 27-48). We will then have an example of the most powerful kind of generalization — revealing a pattern in nature existing at all scales. Poincaré tells us that, throughout the history of changing laws, the “frames ” through which we view nature are stretched into broader generalizations that give us a better perspective (through new laws) of nature’s entirety. Yet nature remains the same.
In the 3 Standard Stoppages, Duchamp takes the three threads and uses Poincaré’s scheme to verify probabilistic systems of chance. Duchamp writes,
The Idea of the Fabrication
— if a straight horizontal thread one meter long falls from a height of one meter onto a horizontal plane distorting itself as it pleases and creates a new shape of the measure of length
— 3 patterns obtained in more or less the similar conditions: considered in their relation to one another they are an approximate reconstitution of the measure of length.
— the 3 standard stoppages are the meter diminished (Bonk, 1989, p 218). (Emphasis original).
Duchamp emphasizes that it is the relation among the three thread events, in approximate reconstitution of his measure system, that “diminishes ” the authority of the meter. Duchamp tells us that his new measurement scheme is, like Poincaré’s, a qualitative system taking the approximate relation among events as the measure, instead of the quantitative method of the meter. Duchamp states:
I’d say the Three Stoppages of 1913 is my most important work. That was really when I tapped the mainstream of my future. In itself it was not an important work of art, but for me it opened the way — the way to escape from those traditional methods of expression long associated with art … For me the Three Stoppages was a first gesture liberating me from the past (Moure, 1984, p 232).
Elsewhere, Duchamp elaborates on this:
This experiment was made in 1913 to imprison and preserve forms obtained through chance, through my chance, at the same time, the unit of length: one meter was changed from a straight line to a curved line without actually losing its identity (as) the meter, and yet casting a pataphysical doubt on the concept of a straight line as being the shortest route from one point to another (d’Harnoncourt, McShine, 1973A, pp 273-274).
Duchamp’s idea seems similar to that of Poincaré (1902/1952) demonstrating that the curved space of non-Euclidean geometry, and the different convention of straight lines in Euclidean geometry, yield two worlds that are connected and interchangeable in the mind, given familiarity with the rules of both systems and the right geometric method for moving from one system to the other (Poincaré, 1902, p 43). 6 Duchamp states that he captured and froze the three thread forms — and that, despite the general laws of chance, and the chance in his individual efforts, similarity and continuity remained evident across the forms. The line of the meter (Euclidean) smoothly meets, in continuity, the curves of another new geometry (non-Euclidean). The new geometry teaches us, as Duchamp stated, that we should doubt any single system, for even though the smooth curves of the threads meet the lines in continuity, the differences are important. Duchamp gives the key case that distinguishes the new geometries (with non-Euclidean and Poincaré’s new qualitative methods as examples) from the old, Euclidean, metric quantitative system. Duchamp states that even though the meter doesn’t completely “lose its identity ” (meaning that, from the perspective of the new, we can still see the old), our “doubt ” must lead us to give up our belief in the absoluteness of the old perspective of the meter. The new perspective of non-Euclidean geometry in Duchamp’s experiment, demonstrates (as the discovery of non-Euclidean geometry actually did) that “the shortest route from one point to another ” in curved space is not a line.
Poincaré had argued that, to do empirical science, we must do experiments, and from these experiments create new measuring systems. Duchamp, in the 3 Standard Stoppages, performs his experiments and derives a result that makes a qualitative measurement system sensitive to relations among events of chance despite coexisting differences. Duchamp’s measuring sticks, based upon the lines and curves created by the chance dropping of threads, becomes his new qualitative system (measuring sticks that he used later in his Large Glass and
Tu m’ painting.) His wooden qualitative meter sticks “measure ” by indicating similarities or unities across scales, despite chance and complex variations or irregularities.
This process of mending similarities among events (individual facts and perspectives) is analogous to the invisible mending (as in the French word stoppage) of perspectives in the unconscious. One might say that an invisible mending among events, despite their differences, represents what we must do to make any generalization. The important thing is to choose an emerging similarity that floats above apparent differences. The 3 Standard Stoppages is a tool box for making generalizations. We have both a readymade (from Duchamp’s unconscious mind) that he used to test his Poincaré discovery, and his actual measuring system within the creative process for detecting new generalizations emerging from facts. Since laws and generalizations come and go, Duchamp has poetically given us the tools that he or anyone needs for making discoveries — experiments (three trials resulting in three facts that allow us to generalize), and new meter sticks (to measure qualitative similarity needed for making generalizations).
In encountering Duchamp’s readymades, we must use the verification system contained inside the 3 Standard Stoppages before we can make a generalization. For, as we learn from Poincaré (1908), one must take a readymade idea and verify it by experiment and measurement. If we use our minds, we can mend (hence Duchamp’s use of the French word stoppages) the relations among what seem to be separate events or facts of Duchamp’s words and works. Poincaré revealed meaning in the relation of gaseous molecules, dust in fluid, pendulums, and the Milky Way, allowing us to view all their phenomena all as related “unstable equilibriums. ” Poincaré goes on to say that the unconscious chooses a readymade idea that must be systematically verified by measure and experiment before being declared a discovery. Duchamp gives us the same set of facts, but not placed in relation. These facts may be separate, confusing and seemingly unrelated in our perspective, but need not be random, unrelated ideas in another viewpoint. The right choice of facts will reveal a relation and new perspective of order within the whole. Poincaré’s probabilistic system of chance gives us this fact and new perspective.
Duchamp scholar William Camfield (1991) discusses Duchamp’s determination to maintain a constant relation between his Large Glass and three of his readymades: 50 cc’s Paris Air (at the top of the stack), the urinal (at the bottom), and the traveler’s folding item (typewriter cover) in between, and located on the line separating the Bride and the Bachelors (called the Bride’s clothes — see Illustrations 1A and 1B)

miniature replicas, photographs and color reproductions of
Duchamp’s work. 40.7 x 38.1 x 10.2 cm. (Courtesy of
anonymous private collection)

Museum, Los Angeles, 1963, in front of
readymades displayed according to their
presentation in his Bôite-en-valise, Photograph.
(Courtesy of Julian Wasser)
. 7 Duchamp kept this consistent relation in his Bôite (the three readymade miniatures are similarly stacked, and placed to the left of the Large Glass), and in his exhibitions in Pasadena and Stockholm at full scale. When Duchamp asked why he wanted this relation between these readymades and the Glass, he said: “because they were ‘readymade talk’ about what was going on in the Large Glass ” (Camfield, p. 165). Certainly we know now that the readymades spoke loudly about their deceptive perspectives which, if seen in the correctly chosen perspective of Poincaré’s mechanism, leads us to understand what the Large Glass really is — a 3-D slice of a 4-D creativity machine.
When specifically asked why the typewriter cover occupied the level of the line or “Bride’s clothes ” (in between the Bachelors and Bride), Duchamp stated, “Oh, it was removed from its machine ” (1991, p. 166). The double meaning of machine (typewriter and Large Glass) is typical of Duchamp’s humor. However, with Poincaré’s theory in mind, we can reach several conclusions: First, he three readymades are probably analogous to Poincaré’s three scales of universal probabilistic systems that Duchamp also uses in his Large Glass; gaseous molecules (50 cc’s Paris Air, at microcosmic scale), dust in fluid (the typewriter cover at human scale) and the Milky Way (the Fountain urinal as part of the universal water system at macrocosmic scale).8 Duchamp’s use of the Bride and Bachelor metaphor for universal creativity relates directly to the metaphor used by Poincaré to explain how and why laws change while nature stays the same. He states that laws act as “frames ” and are the only means to perceive nature. Poincaré literally said that we periodically change the “garb ” or “vestments ” in which we “clothe nature ” with broader perspectives or generalizations. But “she ” (nature) always remains the same (Poincaré, 1902, p 161-162, p 145, 1904, p 95, 139). Poincaré gives the various scales of probabilistic systems including “the pendulum ” as his example of this “parallelism ” (p 161-162). 9
Poincaré’s metaphor, in relation to Duchamp’s, reveals that: the Bride is nature, a probabilistic system at all scales; the bachelors, with their sieves, are discoverers. Most Bachelors, as molds, are vessels in which only old ideas can be cast and cut up to be recycled. They live as a “cemetery ” of liveries and uniforms (nature’s old clothes), dead fixed beliefs acting as old uniforms of convention that we unthinkingly wear (and act as old molds where old ideas are cast). The sieves in contrast, can periodically “strip the Bride ” of old laws in which we dress her by the chance choice of a better perspective within this creative continuum ( “every fifty years ”). 10
The typewriter cover is literally made of rubber. Laws that are stretched until they change, but never completely break, every fifty years act like rubber. If nature is essentially made of raw facts that we can never directly access except through laws, and if the “Underwood ” typewriter cover represents the rubber-like flexibility and persistence of law, then perhaps the Underwood cover is, by analogy, under nature’s facts (Under Wood) and over the invisible creativity machine. [According to Schwarz (1969, p. 146), Duchamp said that the Large Glass “is like the hood of an automobile that covers an invisible motor. ”] Taking Duchamp’s dimensional analogy, the raw facts of nature, in totality, would be 4-D (as they are vast and unaccessible to the senses). Laws are 3-D and visible at human scale (as they represent the means to see nature), and the creativity mechanism (the “sieves ” for both Poincaré and Duchamp) that chooses the law is also 4-D and unseen. Note too that typewriters are also a common device for creating ciphers. In fact, a famous and supposedly “unbreakable ” typewriter “code ” was popular at the beginning of the 20th century. (The code was broken, of course. 11
From Poincaré’s descriptions, Duchamp would have known that a probabilistic system operates like a cipher. Simple initial conditions (a message) in a probabilistic machine are generated, and through time become very complex and seem jumbled. But a relation (in a cipher, or probabilistic initial conditions, or Duchamp’s notes) is maintained and can be deciphered with the right technique. See Illustration 2B.
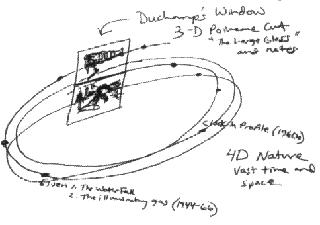
Poincaré Cut for drawing 4-D space. (Author’s Illustration).
Duchamp’s notes orbit from his initial conditions. A Poincaré cut allows us to decipher the relations between the readymade orbits and the initial conditions of Duchamp’s mock probabilistic system. With this relation of readymades and initial conditions (notes) in mind, we can now see the role of the Large Glass as a Poincaré cut. In telling us that the readymades came out of his Large Glass machine, Duchamp relates the readymades to his Large Glass, just as Poincaré relates readymades to the overall creative process (the readymades begin in the unconscious mind as “gaseous molecules ” chosen by “sieves. ” After dropping into the conscious as “sudden illuminations ” they must be “verified by measure and experience ”). The readymade, in this sense, like the projections of 2-D shadows from a sphere, lead us to mentally see that the Large Glass is the universal 4-D creativity machine we are meant to discover. No wonder Duchamp said his readymades “look trivial, but they’re not … they represent a much higher degree of intellectuality ” (as cited in Roberts, 1968, p. 62).
But how can the Large Glass be “four-dimensional ”? Duchamp’s seemingly contradictory statements about the 4-D as physically unseeable, while maintaining that his Glass (which we do see) is 4-D, provides a major clue to what the Large Glass is! We can see from evident perspective that the Large Glass rendering is obviously a three-dimensional representation. The fact that we can see it with our senses at all indicates — especially since Duchamp said the fourth-dimension can only be seen by the mind — that the Large Glass must be three- not four-dimensional. If Duchamp wanted to represent Poincaré’s creativity “machine in motion ” and unconscious sieves as a fourth-dimensional object, how could he logically ever depict it in 3-D so we could actually see it? The answer, of course, resides in the device of the Poincaré cut itself. Poincaré specifically developed this technique as a method for capturing momentary “snapshots ” of overwhelmingly complex, non-linear probabilistic systems that are impossible to see physically in 3-D (Peterson, pp. 160-165).
To summarize, Duchamp described his Large Glass as four-dimensional; the fourth dimension cannot be physically seen, yet we see the Glass in three-dimensions. The Poincaré cut itself can translate a fourth-dimensional system that we can’t see into a lower third-dimensional slice that becomes visible. Look at Illustration 2B. Objects in irregular orbits from Duchamp’s initial conditions, although separating from each other in trajectories generated from initial conditions in time and space, eventually return to a 3-D slice in an unstable 4-D equilibrium. This reduction of 4-D mentality (in Duchamp’s chosen metaphor) to 3-D visibility represents a new application of Poincaré’s technique — a device that was conventionally used to translate 3-D systems to 2-D cuts or 2-D systems to 1-D cuts. Duchamp stretched Poincaré’s dimensional technique to suit his belief that processes beyond the senses — i.e., those that can only be mentally comprehended — are 4-D, whereas visible objects and schematics are 3-D and 2-D. In a note, Duchamp defends his right to extend Poincaré’s technique to include the fourth-dimension in a dimensional continuum [Duchamp always said that he wanted to “stretch ” the laws of physics just “a little ” (Tomkins, p. 34)]. Duchamp writes:
Poincaré’s explanation about n-dim’l continuums by means of the Poincaré cut of the n-1 continuum is not an error. It is on the contrary confirmed and it is by even basing oneself on this explanation that one can justify the name of the fourth-dimension given to this continuum of virtual images in which the Poincaré cut could only be obtained by means of the 3-dim’l prototype object considered in its geometric infinity (Sanouillet & Peterson, p. 98). As shown in Illustration 2B, the Large Glass is a 3-D Poincaré cut of Duchamp’s probabilistic system based on his initial conditions. It is also a cut of the larger universal system of creativity. Now look at Illustrations 2A

and 2B, which compares the window of Leonardo’s perspective system to Duchamp’s Poincaré cut of his probabilistic system. Duchamp had said that “my landscapes began where DaVinci’s ended ” (Roberts, pp. 46-64). Leonardo’s 2-D windows capture the projections between a 3-D singular landscape and the 3-D retina in a perspective system of straight lines (a one-to-one map capturing static reality). Duchamp’s 3-D window is a geometric “snapshot ” (Poincaré cut) of a 4-D probabilistic system of nature’s whole, encompassing a mix of random and occasionally emergent ordered movements in vast times and space — movements that appear overwhelmingly complex and are, for the most part, and with the exception of limited slices, unseen.
Just as the draft piston dots represent return movement on a 2-D plane from the larger 3-D probabilistic system of the Milky Way cloud in the Large Glass Bride, the Large Glass (appearing as a 3-D whole) is a Poincaré cut of the 4-D universal creativity machine, where Duchamp’s specific probabilistic system represents one part in the same continuum. See Illustration 3.
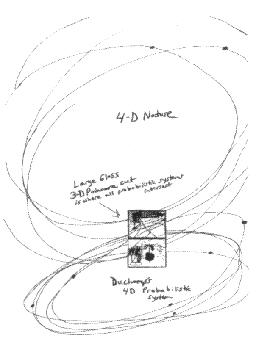
Cut, where probabilistic systems intersect.
(Author’s Illustration)
The whole of nature stands outside Duchamp’s 3-D cut, but the cut is also embodied within, capturing a slice of nature’s whole. Leonardo’s windows are two-dimensional cuts or “snapshots ” of a static, 3-dimensional nature. Duchamp’s window begins where Leonardo’s ended. Duchamp’s window goes beyond 3-D nature and the retinal, allowing us to see into the vastness of nature’s creativity through his non-retinal representation of this vastness as a cut (an abstract schematic “snapshot ”).
Duchamp said that he hated “repetition ” and rejected simple cause and effect explanations of causality and Newtonian determinism. Duchamp correctly said that “formulas and theories are based upon repetition ” (see DeDuve, 1991, p. 238; Gold, 1958, Appendix 41). This statement had been true until Poincaré’s probabilistic system of chance. In an unstable equilibrium, one can discover definite patterns with a Poincaré cut. These “return trajectories ” are not exact, but only similar, and by definition, can never be the same. In Poincaré’s mechanism, Duchamp found a creative machine that couldn’t repeat movements. His ideas and objects would emerge and disappear through time and space, and always stay similar across all scales of nature.12 Duchamp’s ideas were generated from his initial conditions (notes), and then emerged as a variety of words, schematics and objects (never art).
Duchamp made a well-known statement about chance. He states:
I don’t think that the public is prepared to accept it…my canned chance. This depending on coincidence is too difficult for them. They think everything has to be done on purpose by complete deliberation…in time they will come to accept chance as a possibility to produce things. In fact, the whole world is based on chance, or at least is a definition of what happens in the world we live in and know more than any causality…if I do propose to strain a little bit the laws of physics…it is because I would like you to think them unstable to a degree (Roberts, p. 62).
Duchamp asserts that: (1) the world is based on chance (Poincaré’s view of probabilistic systems); (2) his mechanism, along with chance, can be used to produce objects (precisely what Duchamp did with his Large Glass, notes and readymades); (3) as a consequence of accepting fixed perspective and the limited Newtonian “cause equals effect ” explanation of causality, the public is not used to the concept of chance as a means for creativity. Spectators don’t yet know the new, broader perspective of Poincaré’s probabilistic machines, where simple cause and complex effect are unlinked but still related, albeit non-linearly; and finally, (4) Duchamp tells us that he wants to strain laws of physics and mathematics (Newtonian cause and effect) to let us know that, from Poincaré’s new perspective, the phenomena of nature, and the laws themselves, are in fact literally unstable and subject to chance! As Duchamp stated, his “interest ” in “pure chance ” (of probabilistic systems) was “a means to combat logical reality ” or the fixed, limited perspective of determinism (DeDuve, p. 248).
So when Duchamp says that the readymades “are completely different from the Large Glass ” and that there is “no common denominator ” among them, 13 this is literally true — for whether in nature’s return orbits from her initial conditions, or in Duchamp’s readymades from his initial conditions, or in the choice made by the unconscious from its random combinations of gaseous molecules — whatever probabilistic example you use, no two facts are the same. So therefore we must focus on the relations among facts or objects — according to Poincaré, the only aspect of nature’s reality we can know (Poincaré, 1902, p. 20).
When Duchamp told us that the fourth-dimensional Large Glass is open to all perspectives or “interpretations, ” he didn’t mean that all choices are equally valid. (Hulton, March 28, 1965). 14 He meant that ina probabilistic system of creativity, an overwhelming number of perspectives are possible (as he demonstrated, and we experienced, in Apolinère Enameled). The trick of creativity as known by both Duchamp and Poincaré, allows us to choose the best perspective among all the possible viewpoints and never to blindly accept a readymade “idea ” without using your croquet box. 15
I’m not offering an absolute truth in my new interpretation. I’ve learned too much from Duchamp and Poincaré to make that mistake. I believe that my new perspective on readymades and the Large Glass (after examining all the alternative theories including alchemy, the Dada joke, and the theory that “there is no theory ”) represents the best choice among “possible ” perspectives. Why? Because this new perspective forges a new unity in Duchamp’s words and works. In science, gaseous molecules, dust in fluid, and the Milky Way seemed unrelated until a new perspective demonstrated unity. Poincaré’s universal probabilistic mechanism of chance demonstrates a unity that we have not known before among Duchamp’s comments on creativity and dimensionality, Poincaré cuts, unstable equilibriums, readymades, the Milky Way, gaseous molecules, dust in fluids, pendulums, sieves, etc. The list of similar relations between Poincaré and Duchamp goes on. Coincidence? Hardly a reasonable assertion, for our experience, even in this brief essay, shows that single facts shared between Poincaré and Duchamp (they both use the term “sieves ”) aggregate into larger relations ( “sieves sifting illuminating gas ”), into even larger relations (of “unconscious choice, ” “sieves ” sifting “illuminating gas, “readymades, ” “mental beauty, “ discovery and change every “fifty years ”) — all steps of Poincaré’s creativity process within the universal probabilistic system of chance.
The key to my thesis is not a claim that Poincaré was the major influence on Duchamp’s career, but that the master work of Duchamp’s life, the Bride Stripped Bare by Her Bachelors, Even (the Large Glass), and the Green Box Notes of the same name, represent the “mock ” universal probabilistic system that Duchamp created and left for us to discover. When we encounter such overwhelmingly similar patterns, (as listed just above) we are led to make a new generalization — which I have done here as the basis for this essay. Duchamp said that he wanted to be the “champion of the world or champion of something ” and to create something new that had never been done before (Schwarz, 1969A, p. 59). Poincaré’s probabilistic system of chance offered a new perspective never applied before in art or science. (Poincaré’s ideas didn’t begin to get translated into chaos theory until the 1960’s!)
As with the case of impossible figures, Duchamp’s application of probabilistic systems of chance came 50 years before scientists recognized the power of the concept. Probabilistic systems, as part of the discipline of chaos theory and non-linear dynamics, sets a perspective that many mathematicians and scientists have recently adopted and are now busy applying to their work. Croquet boxes, everyone!
NOTES Part II
BIBLIOGRAPHY Part II
Adcock, C. [1984, Fall]. “Conventionalism in Henri Poincaré and Marcel Duchamp.” Art Journal, pp. 249-258.
Bonk, E. [1989]. Marcel Duchamp: The Box in a Valise. New York: Rizzoli.
Buskirk, M. [1996]. “Thouroughly Modern Marcel.” In M. Buskirk & M. Nixon [Eds.] The Duchamp Effect [pp. 191-204]. Cambridge, MA: M.I.T. Press.
Cabanne, P. [1967]. Dialogues With Marcel Duchamp. London: DaCapo Press.
Camfield, W. [1991]. “Duchamp’s Fountain: Aesthetic Object, Icon, or Anti Art?” In T. DeDuve, [Ed.], The Definitively Unfinished Marcel Duchamp [pp. 133-178]. Cambridge, MA: M.I.T. Press.
De Duve, T. [1991]. [Ed.], The Definitively Unfinished Marcel Duchamp. Cambridge, MA: M.I.T. Press.
d’Harnoncourt, A., & McShine, K. [1973]. Marcel Duchamp. New York: The Museum of Modern Art.
Diacu, F., & Holmes, P. [1996]. Celestial Encounter: The Origins of Chaos and Stability. Princeton, NJ: Princeton University Press.
Duchamp, M. [1960]. “The Bride Stripped Bare by Her Bachelors, Even.” In a typographic version of the Green Box Notes by Richard Hamilton: London: Hansjörg, Mayer, Stuttgart.
Gold, L. [1958]. A Discussion of Marcel Duchamp’s Views on the Nature of Reality and Their Relation to the Course of his Artistic Career. Unpublished bachelor’s thesis, Princeton University, Princeton, NJ.
Krauss, R. [1991]. “Where’s Poppa?” In T. DeDuve, [Ed.] The Definitively Unfinished Marcel Duchamp [pp. 433-479]. Cambridge, MA: M.I.T. Press.
Kuh, C. [1905]. In The Artist’s Voice: Talks with Seventeen Artists [pp. 81-93]. Harper & Row.
Maharaj, S. [Ed.]. [1996]. “A Monster of Veracity, a Crystalline Transubstantiation: Typotranslating the Green Box.” In M. Buskirk & M. Nixon [Eds.], The Duchamp Effect [p. 68]. Cambridge, MA: M.I.T. Press.
Moure, G. [Ed.]. [1984]. Duchamp. Madrid, Spain: Sala de Exposiciones de la Caja de Pensiones.
Peterson, I. [1993]. Newton’s Clock: Chaos in the Solar System. New York: W.H. Freedman.
Poincaré, H. [1952]. Science and Hypothesis. New York: Dover. [Original work published in 1902]
Poincaré, H. [1908]. Science and Method. New York: Dover.
Roberts, F. [1968, December]. “I Propose to Strain the Laws of Physics.” Art News 67[8], p. 62. New York: W.H. Freedman.
Sanouillet, M. & Peterson, E. [Eds.] [1973]. Writings of Marcel Duchamp. New York: DeCapo Press.
Schwarz, A. [1969a]. The Complete Works of Marcel Duchamp. New York: Harry N. Abrams.
Shearer, R.R. [1997]. “Marcel Duchamp’s Impossible Bed and Other ‘Not’ Readymade Objects: A Possible Route of Influence from Art to Science” [Part I]. Art & Academe, 10[1]. pp. 26-62.
Shearer, R.R. [forthcoming]. Why the Readymades Aren’t Readymade. Decoding Duchamp’s Paradigm Shift. New York: Springer-Verlag.
Tomkins, C. [1965]. The Bride and the Bachelors. New York: Viking Press.



