Marcel Duchamp’s Impossible Bed and Other “Not” Readymade Objects: A Possible Route of Influence From Art To Science / Part I / Part II
by RHONDA ROLAND SHEARER
Part I of Rhonda Roland Shearer’s essay
was originally published in
Art & Academe (ISSN: 1020-7812),
Vol. 10, No. 1 (Fall 1997): 26-62.
Copyright © 1997 Visual Arts Press Ltd.
IN 1958, Lionel and Roger Penrose published a paper announcing their discovery of impossible figures, (Penrose & Penrose, 1958). These impossible figures formed a new class of visual illustrations, specifically demonstrating a foible in human perception of dimensionality in representations. If we are given a conflicting but balanced mix of visual clues, our logic in two-dimensional representations becomes overwhelmed, and we can easily be fooled about what is possible or likely in three dimensions. The rendered object, on the one hand, looks right; but on the other hand, our intuition tells us that something must be wrong and signals us to use our minds. Our faulty senses always win.
When we do use our minds, we can see how Penroses’ visual ambiguity is created . (see illustration 1)

permission of J.A.F. deRijk, from Ernst, 1996, p. 49.)
The far corners of the cube rise and push away. Further analysis reveals impossible “overlaps” and corner joinings of the bars compared with an actual cube in three-dimensional space. Visual clues lead to conscious expectations. Whether or not these clues conflict, our unconscious minds process them and apparently make a best guess of prediction for interpreting what we are seeing. The confusion introduced by illogical depth signals (between two and three dimensions) is artificial, because the brain does not normally have to deal with this kind of ambiguous object in the everyday world. Based both on apparent “rules” of how the world works and our prior experience of objects and representations, our unconscious guesses are generally so good that, for the most part, our expectations match reality. But impossible figures (and visual illusions in general) prove that perception is less a direct translation of reality than a complex interaction between the eyes and brain, creating only a limited representation of a reality that we believe to be true based on our experiences (Gregory, 1979).
Much mischief can be created by someone aware of how vulnerable we are to mixed depth clues in representations, and, more broadly, to the wide gap between the seduction of the obvious (“seeing is believing…if it looks like a duck…then it’s a duck”) and critical thinking (“but is it a duck?”).
Scholars have documented many cases wherein artists have been influenced by science. Escher (1986, p. 78), most famously, made extensive use of Lionel and Roger Penrose’s concept of the impossible figure in numerous prints and credited their 1958 article as the source of his inspiration.1 Yet, what about instances of scientists being influenced by artists? Examples from art history are difficult to locate. The development by artists of a Renaissance perspective immediately comes to mind-and this discovery did lead to scientific innovations in navigation and technology. However, perspective is not a fair example, because art and science were not as yet recognized as separate categories in the Renaissance, and, in the case of perspective, the new geometry was developed by people who were considered to be both artists and scientists.
Let us consider Marcel Duchamp’s famous “rectified” readymade Apolinère Enameled, created in 1916-1917 (see illustration 2).

plate on cardboard. Note: Metal bed is a seperate piece and attached
to the sign’s surface. (Courtesy of anonymous private)
Duchamp tells us that this work is an enamel paint display sign that he acquired and for which he then changed the text at the top and bottom. Duchamp also claims that he added the “missing” reflection of the back of the girl’s head in the mirror above the dresser. He does not indicate the significance of the piece; nor does he say much else beyond expressing disappointment that the poet Apollinaire (who, we assume, was the “namesake” of this piece and who died in 1918) had not seen it.
Several scholars have noted that something is “wrong” with the bed, the best analysis being that of Andre Gervais (1984). Despite observations that the bed was “out of whack,” no scholar has considered the historical relationship between this fact and the Penrose discovery. 2 Duchamp’s bed is, in fact, a classic example of an impossible object done in 1916-1917, yet the Penroses’ paper was published in 1958! Duchamp’s example predates the Penrose discovery by forty years.
One must ask: could the Penroses have been influenced by Duchamp’s bed? My research, although not conclusive, offers strong circumstantial evidence that the answer may be “yes.” If such is the case, we have located an unusual example of an artist’s influence on scientists. Until now, Duchamp has only been credited with having been influenced by scientists and mathematicians-namely, Poincaré and various texts on perspective (Adcock, 1984; Henderson, 1983).
As in a British detective story, our investigation of a possible Apolinère Enameled/impossible figure connection carries us back to 1958, the date of publication of the Penroses’ article on “impossible figures.” Lionel and Roger Penrose’s close relative, Roland Penrose, was a well-known British artist and was the first British collector to own Duchamp’s works. 3 Materials owned by Roland Penrose included Duchamp’s Box in a Valise, a miniature museum enclosing all of Duchamp’s major works in a collapsible portable display case. This Bôite en Valise, as it is also known, was eventually produced in an edition of three hundred and included, among its sixty-eight works, a reproduction of Apolinère Enameled.
The year 1958 was a busy time for Duchamp in England. British artist, Richard Hamilton, had proposed to Duchamp that he create a typographical version and translation of the famous Green Box Notes. Duchamp had visited Roland Penrose’s house and knew him very well (R. Hamilton, personal communication, Fall, 1997). 4 In the meantime, Hamilton himself was often at Roland’s home. Lionel and Roger Penrose enter the story at this point. Tony Penrose (personal communication, Fall, 1997), Roland’s son, testifies that Duchamp was at their home on more than one occasion. 5 More significantly, Roger, and especially Lionel Penrose, were often at Roland’s as well, playing chess and engaging in lively intellectual conversations. According to Tony Penrose, discussions of optical illusions, a subject that greatly interested both Roland and Lionel, inspired them to treat the topic in their writing (Penrose, 1973).
Thus, as the detective announces before confronting the suspect in a murder mystery, we have motive, means and opportunity. Given Lionel and Roger Penrose’s shared interest (also held by Roland) in visual illusions (motive); their frequent meetings (opportunity); and Roland’s apparent enthusiasm for Duchamp’s work (means); it is likely that Roland Penrose showed Lionel and Roger the Apolinère Enameled work before or at the time of the 1958 publication of their discovery. If Lionel and Roger had, in fact, seen the bed in Apolinère Enameled before their publication, two interpretations seem plausible: (1) they saw the bed in 1958 but did not notice its status as an overt example of an impossible figure before they wrote their article; or (2) they noted the bed, talked about the phenomenon of ambiguity in dimensional representation and then devised and published the general category of impossible figures. I vote for the second. In a recent conversation, Roger Penrose told me that he was familiar with the idea that Apolinère Enameled was an impossible figure, but did not remember when he first recognized this (personal communication, Fall, 1997). Tony Penrose agrees with me that the second scenario seems more likely, and that his father probably discussed Duchamp’s optical illusions with Lionel and Roger in the course of the brandy and chess conversations that often took place in his family home.
I have no smoking gun, but all the circumstantial evidence leads to the conclusion that Lionel and Roger Penrose’s scientific discovery may have been influenced by the artist Duchamp. The dates speak for themselves. Duchamp deliberately used a distinctive example of an impossible figure in 1916-1917. Duchamp’s knowledge and artistic expression of the phenomenon of ambiguity in dimensional representations thus occurred some forty years before the Penrose article. Moreover, the year that the Penroses published their paper was the very same year that they probably had seen Duchamp’s bed at Roland Penrose’s house. This fact, however, does not detract from the importance of the Penroses’ discovery. Duchamp’s demonstration provided one example of an impossible figure. 6 The Penroses joined this with an entire category of optical illusions and coined the term “impossible figure.” My point here is only to suggest one possible influence of an artist’s work upon a scientific discovery. The more typical course of influence runs the other way, from science to art, as is well documented in art history.
Duchamp himself had an intense interest in perceptual ambiguity and optical illusions and constructed a number of scientifically original related devices and machines. 7 In 1935, he entered an annual Paris inventor’s salon with his Rotorelief discs-cardboard circles designed to be spun on a phonograph turntable (d’Harnoncourt & McShine, 1973, p. 15). The varied designs appear to lift spontaneously and to recede between two and three dimensions. From his twelve Rotorelief designs, we would not, at first, suspect that these discs were anything more than a two-dimensional pattern. Only from another perspective, that of the discs actually spinning, does this two-dimensional design surprise us-as we learn that the flat, two-dimensional image can become dimensionally unstable, seeming to change with its movements from two to three dimensions and back again. A Rotorelief was, in fact, included in the Bôite en Valise, providing another optical illusion piece by Duchamp that might have prompted Roland Penrose to share his Bôite collection with Lionel and Roger Penrose. 8
The story of Apolinère Enameled not ony records an artist’s possible influence on a scientist’s discovery, it also marks, like the rest of Duchamp’s life and work, a possible influence of science upon an artist. Duchamp said that he acquired the Sapolin sign for Apolinère Enameled and altered the letters. Despite vigorous research and detective work, no other copy of this sign has ever been found. The closest example, discovered by artist Sherrie Levine, was a Sapolin paint sign, with the same bed and similar lettering, but with only a plain black background (see illustration 3).

cardboard, wood frame (Sapolin Enamel Advertising Sign)
18″x11″x1″. (Courtesy of Francis M. Naumann, private
collection.)
9 We can easily surmise why the bed was given its peculiar form by the paint company. Even though the bed is an “impossible figure,” it was obviously rendered this way (without an interruption of the footboard’s rungs by the back mattress rail) for greater ease in stamping out the metal form from a template. Duchamp’s eye must have seized upon the resulting transition from manufacturing necessity to perceptual absurdity as a good example of how a dimensional representation or individual fixed perspective fails to embody truth in nature, forcing us to actively employ our minds to “see.”
Duchamp, throughout his life, insisted that he hated “retinal art,” preferring the “non-retinal beauty of grey matter” (Schwarz, 1969a, pp. 18-19). Given his insistence that the reafymades were “completely grey matter,” Duchamp continued to be amazed that people stubbornly praised their beauty (as in the tradition of “retinal art”) – in direct opposition to his pronouncements (see Hulton, 1993-June 21, 1967, Camfield p. 164 10). In fairness, Duchamp never explained how the cerebral beauty of the “moves,” “patterns” and “schematics” that he discerned in both chess and art actually related to his readymades (Schwarz, 1969a, pp. 68-69). He claimed that chess playing and art were unconscious processes, removed from the senses and, therefore, fourth dimensional. 11 Literal chess pieces or other objects were three-dimensional, and any schematic or plan that would map the movements of these three- and four-dimensional ideas or objects (visible or invisible) was two-dimensional. Creativity was a ninety-degree hinged rotation, moving from the four-dimensional unconscious idea to the three-dimensional pattern, with the two-dimensioanl schematic map capturing both and acting as an intermediary between the invisible and the visible-a means of bringing forth a discovery as well as memorializing the discovery in a form for others (“spectators”) to see with their fourth-dimensional minds (Sanouillet & Peterson, 1973, p. 92).
Duchamp states that his readymades, like Apolinère Enameled, the urinal, bottle rack, snow shovel, etc., are “three-dimensional shadows” of his “fourth-dimensional” Large Glass mechanism (see illustration 4 outlining the parts of the Glass) ( as cited in Cabanne, 1967, p. 40).
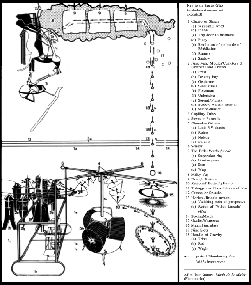
Bare By Her Bachelors, Even (The Large Glass),
1915-1923, created from Duchamp’s notes by Jean
Suquet (includes parts never completed). (Courtesy of
Jean Suquet.) Large View: 100k
The Large Glass (created between 1915-1923) and notes (mostly completed between 1911-1915) 12 were Duchamp’s masterpiece, also entitled The Bride Stripped Bare By Her Bachelors, Even. Duchamp often repeated that to understand his project one had to put the Large Glass and the notes together: “the conjunction of the two things (Glass and Notes) entirely removes the retinal aspect that I don’t like. It was very logical” (as cited in Cabanne, 1967, pp. 42-43).
But how could readymades be third-dimension shadows of his fourth-dimension Large Glass machine? For an answer we can look to the great mathematician of the late-nineteenth and early-twentieth century, Henri Poincaré, who continues to be regarded as one of history’s great mathematicians, was also a famous popularizer of scientific ideas. Many artists, at the beginning of modern art in the early-twentieth century, knew and discussed Poincaré’s works (Henderson, 1983).

three-dimensional object from only the cast shadows in
two dimensions. (Reprinted, by permission, from The
Nature and Power of Mathematics by D.M. Davis, 1993,
p. 138.)
Poincaré had developed a specific geometric technique (see illustration 5), where two-dimensional shadows could be used to express the existence of a three-dimensional sphere without the observer ever actually seeing the three-dimensional object (Davis, 1993, pp. 138-139).13 From a two-dimensional creature’s perspective, by mentally putting together (in a series) the relations of two-dimensional shadows projected from the sphere, we can, through logic, extrapolate and therefore “know” or see in our minds the higher dimensional object.14
Duchamp had also said that he wanted the titles of his readymades “to carry the mind of the spectator towards other regions more verbal” (Sanouillet & Peterson, 1973, pp. 141-142). For Duchamp, one cannot physically see the fourth dimension (Sanouillet & Peterson, p. 98). For two-dimensional creatures, Poincaré’s 2-D shadows would lead to the 3-D sphere only if they were to use the inductive powers of their minds to “see” the existence of a sphere they could never physically perceive. According to Poincaré’s definition of shadow projections, and by dimensional analogy, we should be able to use Duchamp’s 3-D readymade shadows to lead ourselves to the higher fourth-dimensional perspective of the Large Glass. Duchamp defined the fourth-dimension as as beyond direct sensory experience, whereas the second and third dimensions can be experienced by the senses (Sanouillet & Peterson, 1973, p. 98).15 In other words, two-dimensional creatures would have to use their minds to evaluate the relations among the sizes of the shadow circles in order to get to the sphere; and by analogy, we have to use our minds to evaluate the relations among the readymades to mentally “see” or understand what the Large Glass is in the fourth dimension.
Let us return to what Duchamp called his “rectified readymade,” Apolinère Enameled. Think of it as a shadow of the Large Glass, as defined by Poincaré in his projection technique (see Davis, 1993). Will it bridge the different dimensions and enable us to see beyond our three-dimensional limited perspectives to the next higher dimension?
Gervais (1984, p. 115) has made the general observation that the bed is an “impossible object.” One assumes, since he does not cite “impossible figure or object” as a psychological category of optical illusions, that he uses this term as a vernacular description of the perspective problems in the bed without linking them to the Penroses’ formal idea and term. Gervais cites three problems: (1) the right foot of the headboard is attached to the front mattress rail; (2) the back mattress rail cuts diagonally from the mattress rail; and (3) the painted rungs, four in the footboard and five in the headboard, should be equal in number, but are not (p. 115). I had to make a three-dimensional model of the Apolinère Enameled room and objects and do a computer analysis of the entire picture in order to realize that these three problems (that Gervais and I had noticed independently) are not the only examples of false perspective with respect to the bed. Moreover, the entire room-the rug, the dresser, the walls, the girl-is all “out of whack.” (I discovered that even the reflection in the mirror of the back of the girl’s head that Duchamp said was “missing” cannot be right when you consider the necessary angles for reflections and the girl’s closeness to the wall.) Although we accept the whole picture as a Gestalt, each individual object, in relation to the others, exists in an independent world that we have to force ourselves to see.
Faulty depth clues in the bed provide the most obvious “shadow” (analogous to a single circle in the sphere’s projection) of this readymade. Now we must find the others which will, like the series of circles in Poincaré’s projection, follow in a false and deceptive perspective similar to that of the bed. But one immediately finds that it is impossible to simply fix the perspective. You have to choose a part, the headboard or footboard of the bed for example, and then adjust everything else to this choice as a set of projection lines. No single perspective is correct or immediately correctable. We must select one part, adjust the rest to it and create a new whole (see illustrations 6A and 6B).
16 Using the footboard in A and the headboard in B (as my choices), all else in the room shifts. Contrast 6A and 6B with illustration 2 of the original Apolinère Enameled. Note the startling differences. Due to the power of the false perspective clues, you have to fight your retinal vision and force your mind to make careful comparisons in order to see what are, paradoxically, very real and obvious differences that continually slip away from direct perception. Making point by point comparisons, you will be surprised by how “stupid” your vision is, and how willingly (lamb to slaughter) you go along with the seductive power of false and ambiguous perceptual clues.
In order to see the differences between 6A and 6B in the clearest way, I made overhead transparencies of the original Apolinère Enameled and the two changed versions (6A and 6B). Then, two at a time, I held them up to a lamp, allowing the overlay to reveal the differences in locations of the objects thus revealing what is “corrected” from only two perspectives (6A and 6B). (One could play this out in other ways, by choosing the dresser top or the back mattress rail, obtaining very different perspective results each time.) For example, in 6B,

headboard. Compare to Illustration 6A
where the headboard is the fixed object, note that the footboard dips below the picture frame, pulling the side mattress rail toward you. The dresser also dips slightly along with dresser’s top left edge. The footboard version, 6A,

footboard. Compare to Illustration 6B
reveals even more dramatic alterations, as the headboard and girl wheel over to the right and back toward the wall. The dresser, this time, moves up and out of the picture.
James Nazz, the computer graphics specialist who did the computer analysis for me, was amazed. In his efforts to put everything into a “correct” perspective, he quickly realized how “off” everything was despite how “correct” it looked. Upon further investigation, he observed that this effect was created by certain key alterations or “tweakings” made to create a correct appearance and fool the eye. What better test of a spectator’s non-retinal resolve, and what better demonstration of the overt failure of the retinal could we cite, than the deceptive Gestalt of Duchamp’s Apolinère Enameled. But this work represents only one readymade shadow from Duchamp’s Large Glass machine. What about the rest of the series? Do the others similarly deceive our eyes and require our minds in order to see?
Before discussing the other readymades and exploring their important connection to both Poincaré’s notion of “tout fait” (translated as “readymade” in English) and Duchamp’s use of both words (“tout fait” and “readymade”), I want to mention Poincaré’s notion of how the unconscious formulates our perspectives (see Poincaré, 1908, pp. 62-63; Schwarz, 1969a, pp.2, 88, 90). According to Poincaré, we do not live in just one single perspective, but “the aggregate of our muscular sensations will depend upon as many variables as we have muscles. From this point of view motor space would have as many dimensions as we have muscles” (emphasis original). Because we have so many simultaneous perspectives at any given time, all thes views are stitched together and only emerge as one after being chosen and integrated by the unconscious.
This is a good description of what happens to us when looking at Apolinère Enameled. From all the ambiguous depth and perspective clues, our unconscious selects and integrates one view that becomes our consciously accepted reality and disregards the now irrelevant information. In other words, mixed perspective “signals” are sorted through and the most likely one is unconsciously chosen. Upon this selection, the other (now conflicting) signals are downgraded to “noise” and are overridden by the one fixed view. The unconscious “choice” is not a replication of reality, but only a “best choice” among ambiguous clues or signals-a procedure that works well most of the time.
As in illustration 1, the impossible cube example, one ordinarily does not have to see all the corners and edges to note the logical congruence of a typical cube. We can guess. Just as with the sphere projection of shadows, once we learn the shadow pattern from experience, we don not have to actually see the sphere. Interpolation-or filling in the blanks-is the modus operandi of perception. The key, however, according to Poincaré (1908), lies in not accepting everything “readymade” from the unconscious. For no matter how inspired an unconscious intuition might be, Poincaré insists that we still need conscious logic, or to use Poincaré’s exact words, “verification by measure and experiment” (pp. 62-63).
Let us temporarily suspend our attachment to the traditional view that “readymades” mean easily purchased, manufactured objects and consider Poincaré definition of “readymade” as our new hypothesis for what Duchamp meant by the term. We soon see that Poincaré’s definition of a “readymade series” leads us to knowledge of the true mechanism of the Large Glass, just as the series of shadows of the circles leads us to the sphere. Poincaré defines “readymade” as one stage of a larger process of creativity. Moreover, he claims that discovery in any field (art or science) operates identically to the larger-scale, machine-like creativity of universal nature itself.
According to Poincaré (1908), all systems-from the largest (Milky Way) to the smallest (gaseous molecules)-operate like “probabilistic systems of chance) (pp. 254-255). In fact, modern chaos theory is based on Poincaré’s idea of probabilistic systems. Beyond Newton’s simple world view of cause equals effect, in Poincaré’s probabilistic world of “unstable equilibriums,” small differences in “initial conditions” create indeterminate or chance results (Ruelle, 1991, p. 45). Poincaré offers roulette and the weather as examples of these systems: small muscular differences that occur while spinning the roulette wheel can greatly effect, in a way that we cannot measure, the red or black outcome; similarly, the smallest item falling in one geographical location can effect the weather on the other side of the world six months later. Although we may be able to predict that a cyclone will occur, we cannot determine exactly when or where it will occur (Poincaré, 1908, pp. 68-70).
Individual creativity, Poincaré (1908) tells us, operates similarly. There are three distinct steps, and one intermediate step (p. 56). Conscious Step 1 includes the discoverer’s desire, the facts of nature and conventional law as the initial conditions. Unconscious Step 2 entails the disaggregation of these facts of nature, law and desire into gaseous-like molecules which bounce and randomly collide, forming new combinations. 17 The next step falls in between Unconscious Step 2 and Conscious Step 3, where, if you are a genius, unconscious sieves choose the “right combination” while the conscious mind does nothing, and these combinations (gaseous molecules in a new aggregate) drop like “sudden illumination” (converting from gas to ideas) into the conscious mind, as if “readymade” (pp. 62-63).18
Poincaré explains that ideas seem readymade, in part at least, because they suddenly drop from the unconscious mind into consciousness and appear disconnected from conscious effort. But, Poincaré declares, the idea is not “readymade,” nor is it to be trusted and declared a discovery, until Conscious Step 3 is performed-that is, conscious verification by measure and experiment (pp. 62-63). When we adopt Poincaré’s definition of “readymades” as part of a larger creative process that requires both unconscious “intuitive choice” and critical thinking, we are led to conclude that Duchamp’s three-dimensional “readymades” are intended to represent shadows of his fourth-dimensional creativity machine! The Large Glass is an (observable) three-dimensioanl slice of the (invisible) fourth-dimensional universal system of creativity in nature.
Duchamp acknowledged in his notes that he was aware of “Poincaré cuts” (Sanouillet & Peterson, 1973, p. 94). 19 A Poincaré cut is a method invented by Poincaré, similar to his use of two-dimensional shadows, to convey an invisible three-dimensional sphere. A 3-D Poincaré cut allows us to visually represent a moment or “snapshot” of a fourth-dimensional non-linear system that could not be physically seen from our limited, human perspective (Diacu & Holmes, 1996, pp. 34-41) (see illustrations 7A and 7B). A Poincaré cut is a window into a system of chance and complexity, which captures emergent patterns of randomly-generated order. A simple set of conditions may initiate the original process (as in roulette, we begin with a spin of a wheel, gravity, a ball bouncing against metal pins, etc.), but soon the resulting dynamic of actions and effects transcends any obvious connection to the original simplicity of the initial conditions. Similarly, Duchamp, from 1911-1915, wrote an initial set of notes (his initial conditions) from which he generated both a system and all his major work for the rest of his life. For example, “a clock in profile,” first written about before 1915, does not return as an object until the 1960s. The cryptic note, “Given 1. the waterfall, 2. the illuminating gas,” is written before 1915, yet we do not learn of the existence of this work until his death in 1968 (Duchamp, 1960, pp. 3, 4, 94).
By putting out a “net” and mapping return movements within large and small probabilistic systems across time and space (whether these be Duchamp’s creative movements, the movements of the Milky Way or the fluctuations of gaseous molecules) we, in effect, have “tamed chance,” because such maps reveal order within seemingly overwhelming randomness from our 3-D human perspective. Using a probabilistic mechanism for his creativity, initial conditions in Duchamp’s mock system operate just as in roulette, or the weather. Given his original notes (his initial conditions), we can make fairly good predictions. However, neither we nor Duchamp himself could have said exactly what or when. Perhaps this was the joke when Duchamp (1960, p. 97) said he would plan “a kind of rendezvous” with his readymades. 20
People familiar with Duchamp’s writing and works know that he was extremely interested in chance (he even wrote a note about “canned chance”) (Duchamp, 1960, p. 87) Chance, in science, need not be synonymous with the vernacular definition of randomness. During Poincaré’s period-that is, when Duchamp recorded his initial notes in 1911-1915-one common meaning of chance referred to our inability to exactly predict an outcome due to our limited perspective and our incomplete knowledge of nature. Probabilistic systems are called “indeterminate determinism” because if we knew everything we could determine everything; but such knowledge is impossible since the smallest initial variations (which can never be completely known or measured) can create large-scale effects.
Although constraints of length debar me from going into great detail in this essay, I will present evidence indicating that Duchamp’s Large Glass is a “Poincaré cut” of Poincaré’s “unstable equilibrium” of universal creativity. Moreover, I will demonstrate that Duchamp’s “readymades” are three-dimensional shadows from his creativity machine, intended to lead us toward a fourth-dimensional realization of the significance and meaning of his Large Glass.
Before one can discover anything new, one has to suspend present beliefs in order to surpass them. In Poincaré’s mechanism of discovery (and in his striking and admittedly curious metaphor), this leap takes the form of a disaggregation and remixing of gaseous molecules. Duchamp proclaimed that he “doubted everything” (Tompkins, 1965, p. 17) and did not “believe in fixed positions” (Cabanne, 1967, p. 89). How can we believe in a single dominant perspective if, as we have learned from Apolinère Enameled, any one perspective is actually a combination of perspectives chosen by the unconscious, susceptible to error and capable of improvement, as is amply demonstrated by the changing history of ideas. If doubt, as Duchamp believed, is fundamental to the beginning of the discovery process, then perhaps the readymades were the seeds of doubt he sowed. If we find that the rest of the readymades are in the “wrong perspective” and have fooled us, the seeds of doubt should bear fruit in a full-scale inquiry into The Large Glass machine (identified by Duchamp as the source of his readymades.)
When we follow Duchamp’s recommendations and put the Large Glass and notes together (see illustration 4), we see that Duchamp describes, in text and image, a Poincaré machine of chance. Speaking of the “Pendu” Bride in the top half of the Glass, Duchamp tells us, as Poincaré does about his machine, that his “Pendu” mechanism is “extremely sensitive to differences” in “meteorological” influences (Duchamp, 1960, p. 19; emphasis original). The “Pendu” (add -lum for pendulum or -le for pendule, in French) is shaped like a “double pendulum.” Like the weather, the double pendulum is always used as a key example of the marriage of irregularity and order in a chaotic system (see illustration 7B).
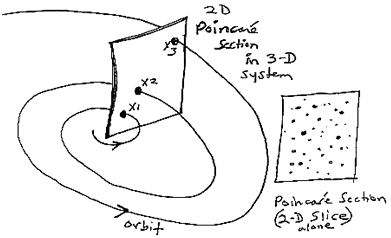
Duchamp’s sketch of his “Pendu” is, in fact, identical to the double pendulum of chaos theory (Peterson, 1993, pp. 160-165).
Duchamp, moreover, uses Poincaré’s exact, technical term “unstable equilibrium” to describe his machine (Matisse, 1980, note 15; Poincaré, 1908, pp. 67-68). The vapor cloud emitted from Pendu’s “swinging to and fro” (Duchamp, 1960, p. 16), he calls the “Milky Way” which, like the pendulum, is an example of a probabilistic system (p. 26). The “draft pistons,” the three window-like cuts in the Milky Way cloud, Duchamp calls the “nets” or “triple cipher” (p. 27). Duchamp claims that he made the draft pistons by using netted fabric with dots and placing the fabric in front of three literal (and open) windows, with air currents blowing through. The three resulting “snapshots” (his words) captured subtle differences in the movements. Chaos scientists similarly refer to “Poincaré cuts” as “snapshots” of probabilistic systems of chance (Peterson, 1993, pp. 160-165). For both Duchamp and Poincaré, it is the initial conditions, and the forces of air resistance and gravity, which create irregular and irrational movement in the pendulum (Peterson, pp. 160-165). For his draft pistons (Poincaré cuts) within the Milky Way (a large-scale probabilistic system), Duchamp mockingly borrows from his Pendu (pendulum) the effects of “air currents” (Duchamp, 1960, p. 18). These currents create irregularities of motion and literally represent all scales of probabilistic systems in nature (vapor as microcosmic, pendulum as intermediary human scale, and the Milky Way as macrocosmic-all scales are impacted by the small effects of their initial conditions).
Look at Duchamp’s three Poincaré cuts in his Milky Way system (see again the cloud shape in illustration 4). They closely resemble the Poincaré cut shown in illustration 7A
see illustration 8

gelatin silver print. Looks like a Poincaré cut. (Courtesy of A.
Schwarz, private collection.)
showing one of Duchamp’s draft piston photographs). Poincaré frequently used the very same examples to illustrate nature’s three major scales: the Milky Way, dust in fluid, and gaseous molecules-all of which are probabilistic systems whose Poincaré cuts would look alike (see illustration 7A).
However random the movement in a probabilistic system, the Poincaré cut proves that something remains constant across vast scales. Poincaré states that this intangible “something” allows us to recognize that, despite any overt changes that we perceive in nature, it is only our concept of nature’s laws that really changes. Nature itself always remains essentially the same. For both Poincaré and Duchamp, the creativity game is played by changing our perspectives in two ways. We may manufacture and choose our perspectives in our unconscious but, at the same time, we must explicitly recognize and challenge our beliefs in order to be able to change perspectives and win the game by making discoveries and innovations. Since “logic proves” whereas “intuition discovers,” we need both conscious logic and unconscious intuition to be creative (Poincaré, 1908. p. 129).
Duchamp’s Large Glass includes all four of Poincaré’s examples of probabilistic systems-the top half of the Bride has the pendulum, gaseous molecules (vapor) and the Milky Way; and the bottom half has dust in fluid and gaseous molecules. Duchamp made the sieves in the Large Glass (see illustration 9)

used real dust in varnish fluid to represent “illuminating gas.”
function just as Poincaré described in his theory of the unconscious creative process. In the Large Glass, the “sieves” are the only visibly active part of the machine. Duchamp used actual dust in lacquer fluid to represent gaseous molecules (“illuminating gas”) in his sieves, employing the same analogy for “invariance” within nature (despite nature’s overt changes of scale) that Poincaré characteristically uses. We note that the dust increases in density from the first to the last sieve. The last sieve occupies that critical point of final unconscious choice of a new perspective which will be launched, as if “readymade,” into the conscious mind of the discoverer.
Following Poincaré’s (1908, pp. 53-55) insistence that readymade “sudden illuminations” and “right combinations” come in rare, limited “series,” Duchamp consciously limited the production of his readymades. Duchamp even wrote a note reminding himself to “limit the number of readymades yearly” (Duchamp, 1960, p. 98).
Before 1915, when he first uses the word “readymade” in direct connection with his objects, Duchamp refers to a “readymade” series, out of his Large Glass machine, as an “operation” of choice (Duchamp, 1960, p. 98; Schwarz, 1969b, pp.2, 88, 90). 21 Duchamp’s emphasis on choice goes back to his 1917 public statement following the rejection of his fountain urinal from the Society of Independent Artists’ Exhibition. Duchamp wrote that the important thing was that “Mr. Mutt CHOSE” it (emphasis original) (Schwarz, 1969a, p. 43). 22 Duchamp, like Poincaré, often repeated that it was the unconscious mind that “chooses.” According to Duchamp, “because the subconscious attends to the choice-in reality everything has happened before your decision” (see Hulton, 1993-Dec. 8, 1961, p. 62). Duchamp states that the “readymade” “chooses you” (Roberts, 1968, p. 62) and is “pulled out” from the unconscious (Clearwater, 1991, p. 53). If we use Poincaré’s definition of the “unconscious choosing” of a new idea or perspective, Duchamp’s comments are no longer contradictory. The “readymade” would seem to “skip earlier stages (of conscious work) and come to its final conclusion,” readymade for verification (measure and experiment by us) just as Duchamp claimed (see Hulton, 1993-June 16, 1966). If the unconscious mind does the choosing, artists are literally “mediumistic beings” in a state of “complete anesthesia” (absence of conscious mind) and would avoid relying upon the “hand, taste or style” which Duchamp frequently stated was his creative goal (Sanouillet & Peterson, 1973, pp. 138, 141).
Duchamp makes the same point when he argues that conscious “indifference” is the “common factor” among all readymades: “if you arrive at a state of indifference…at that moment it becomes a ‘readymade'” (see Hulton, 1993-June 21, 1967). Obviously, if the choice occurs in the unconscious, Duchamp is correct to conclude that “no intention or object is in view” during this selection process, and that readymade ideas are only subsequently “unloaded” into the conscious mind (see Hulton, 1993-July 1, 1996). When Duchamp declared that readymades are “manufactured goods,” he neglected to inform us that the manufacturing was occurring in the machinery of the unconscious (Hahn, 1966, p. 10). 23
Duchamp’s most contradictory statements will be explored later in my paper. For the moment, if we find, as we do, that the Apolinère Enameled is not what it initially seemed to be from the vantage point of our first unconscious choice of perspective, then perhaps, using Poincaré’s definition of readymade, we should critically examine all the other readymade objects to see whether a strategy of consistent “doubt” leads us both to a fuller understanding of Duchamp’s Large Glass (a discovery machine) and to a discovery of our own about the relationship of the readymades to the Glass.
Let us first take Duchamp’s Why Not Sneeze Rrose Sélavy? (1921) (see illustration 10.)

Rrose Sélavy?, 1921, 152 marble cubes, a thermometer, a
cuttlebone, in a small birdcage fitted with wooden bars. (Courtesy
of the Philadelphia Museum of Art, The Louise and Walter
Arensberg Collection.)
He tells us that it is a purchased birdcage to which he added a cuttlebone, marble “sugar cubes,” and a thermometer. Given the skepticism that follows from our investigation of Apolinère Enameled, the suspicion arises that, although we have always accepted the presupposition that Duchamp bought it readymade and did not change it, this assumption is likely to prove false. The evidence that Duchamp did, indeed, alter the birdcage is right before us (see illustration 10). The wires across the top edge have obviously been clipped off and cut to reduce the size of the cage. As in the case of the bed of Apolinère Enameled, we are now looking at an impossible birdcage. Examine the object non-retinally and try to imagine a bird that could fit within this cage. Look at the perches in relation to the cage. What bird could sit on these? Consider also the cuttlebone’s absurd size in relation to the cage-the cuttlebone is bigger than the implied bird should or could be; it towers above the cage, obviously oversized.
What about Duchamp’s snow shovel (1915) (see illustrations 11A and 11B).

readymade snow shovel, photographed
in his studio, 1917. (Courtesy of
anonymous private collection.)

with round shaft handle, 1945. (In Advance of the
Broken Arm, Yale University Art Gallery, Gift of
Katherine S. Dreier to the Collection Societe
Anonyme.)
11A is allegedly the original readymade, photographed in Duchamp’s studio. But look at the shaft. It is square. Now compare this square-shafted shovel to 11B, the snow shovel that Duchamp really did purchase in a hardware store, in accordance with the explicit request of his collector, Katherine Dreier, in 1945 (Schwarz, 1997). The shaft of the snow shovel 11B is round; but every drawing and reproduction since has had a square shaft like the lost original in the photograph. I stared and stared at these shovels, keeping the hypothesis in mind that something was wrong with the perspective. I knew that something looked fishy about the hanging shovel’s size (see illustration 11A). If the bicycle wheel in the foreground is approximately 26½ inches in diameter and the wheel from one of his optical machines (Rotary Glass Plates, 1920) in the background is about 13 inches (these approximate measurements were available), how could the shovel in the middle be full-size in relation to the other measurements? 24 But it was not until I imagined picking up the square-shafted shovel and using it that I realized what was wrong. No wonder that Ducahmp sardonically titled this “readymade” In Advance of the Broken Arm. Hand tools, brooms, and shovels all have round shafts and a slip-in, male into female connection. But 11A, unlike 11B, has a bolt and anchoring sleeve above the shovel blade, attaching it to the handle.
My almost completed research into the history of tools confirms my suspicions that Duchamp changed the snowshovel’s shaft. Duchamp scholar Molly Nesbit (1991) used illustration 12A to demonstrate a typical tool design book from the period when Duchamp was educated in France (see illustration 12A.
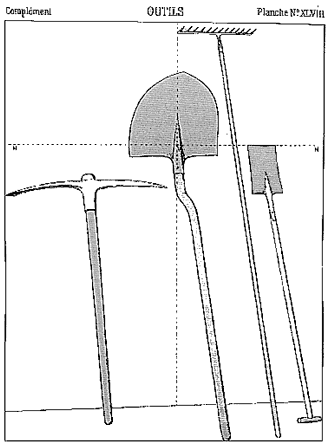
Traditional tools have round shaft handles. (Reprinted, by
permission, from M. Nesbit, 1991, p. 365.)
Note that every real tool looks like snowshovel 11B, the one that Duchamp truly purchased in the store-round shaft handle, and typical male/female connection of shaft to shovel (Nesbit, 1991, pp. 351-385).
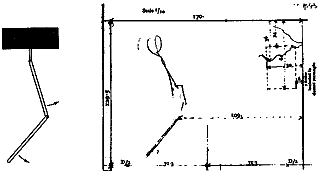
For my study of Duchamp’s Hat Rack (1917) and Trap (coat rack, 1917, titled, Trébuchet, a French word for trap in chess, where a pawn is sacrificed in the interest of a larger strategy), I have completed research on hooks in general and hat racks and coat racks specifically. Hooks, by definition, either go up or run straight. In hundreds of examples, I have never seen a hook curving down (which makes sense, for if you try to hang a hat or a coat on a downward hook, the item is likely to fall off!) (See illustrations 13A and 13B).

in his studio, 1917. (Courtesy of anonymous private
collection.)

in his studio, 1917. (Courtesy of anonymous private collection.)
Duchamp’s hooks go the wrong way! Duchamp admits that he changed the orientation of the coat rack, claiming that he nailed it to the floor because he kept tripping over it. The main hook goes down and the two smaller hooks go up. If we try to turn the coat rack around to correct this, then the two small hooks go down and the large one goes up. (The hooks even vary, the last middle hook is bent up and unusable.)
As he claimed for the snowshovel, Duchamp claims that he lost both the original Hat Rack and Trap (coat rack). What I have illustrated here in 13A and 13B are, allegedly, the originals hanging in his studio. 25 The Hat Rack looks, even at first glance, like a counterfeit. And the perspective shown in the Hat Rack cannot be correct. Look at the distortion and incorrect perspective in the arrangement of hooks illustrated in the Schwarz drawing from the original photo (see illustration 14A).
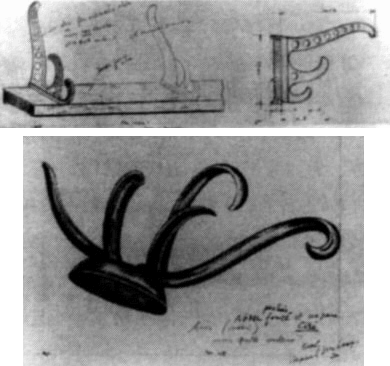
1964, from Marcel Duchamp’s original photographs. (Courtesy of A.
Schwarz private collection.)
How could the false perspective of the drawing and original photograph be translated in the reproduction of a symmetrical “hat rack” with six equal hooks when the drawing and photograph showed five varied sizes of hooks and an impossible configuration, and overlap?
I am presently doing a computer version of Duchamp’s Hat Rack which will display this distortion from different perspectives in order to clarify my point. (See illustrations 14C and 14D

American Hardware Catalogue of Russell and Erwin
Manufacturing Co., p. 85.

1910 Catalogue of Sears and Roebuck and Co.,
p. 125.
for historical examples of hooks from the late-nineteenth and early-twentieth centuries.) In retrospect, Duchamp was right. The coat rack is a Trébuchet, a mental trap, set right in front of us. We trip right over it, missing the fact that the main hook goes the wrong way. We do not see this because our fixed perspective blinds us. We are told that the objects are a coat rack and a Hat Rack and we accept this claim. Duchamp’s Hat Rack should look like the one in illustration 14B,
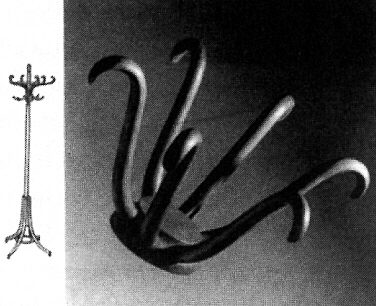
traditional Bentwood hat and coat stand. (Courtesy of A. Schwarz private
collection.)
which is the traditional Brentwood design implied by his Hat Rack. But think about it. Make a mental picture of how 13A would have looked as an original Hat Rack in comparison with the 14B design. Even if we mentally rotate and correct the hooks to go up, what constituted the rest of the hat rack’s total form? What was on top of the hook section structure? How did the hook section connect to a stand below? How could it make sense?
The same applies to the putative original sign from Apolinère Enameled. What did the original ad show? The Sapolin ad that Sherrie Levine found looks right as an ad design. But what about Apolinère Enameled, with a black strip painted above and below to hold text and display the bed? It is difficult to imagine a proper sign with the elements that Duchamp presents to us-bed, text and background painting. Given the complexity and subtlety of the ambiguous perceptual clues, together with the label on the back of the sign, I suspect that Duchamp may have painted the background. The label on the back states, “Wipe off with damp cloth.” Duchamp adds in his own hand, “Don’t do that” (see Bonk, 1918). If the sign were enamel, it could be wiped-after all this is a sign to advertise enamel paint! But perhaps this altered label is a clue that it is not enamel, and that the entire background painting, not just the changed letters at the top or bottom, are done in some other kind of paint. If this is so, could we not conclude that Duchamp himself painted (or had someone paint) the background? 26
What about Fresh Widow (1920), a French window built by Duchamp? Real French windows open out. Duchamp’s Fresh Widow is put into by more than just an incorrect spelling and black covering where glass should be. His French windows in Fresh Widow incorrectly open in, as signaled by the handle pulls and hinges.
As for the rest of the readymades, after considering my hypothesis, a person who requested to remain unnamed told me (personal communication, Fall, 1997) that he had noted that the Bottlerack (1914) seemed to have the wrong number of hooks and “that something seemed wrong” with the Bicycle Wheel on a stool, although he did not know exactly what. 27 When I actually counted the Bottlerack hooks (using Duchamp’s photograph of the “lost original”-a photo that scholars have noted has an incorrect and artificially-placed shadow), I observed that, as compared with his later reproductions, the tiers contain an odd number of hooks, asymmetrically distributed among the four quadrants in each tier of the rack (13, 10, 9, 9, 9, in the five tiers, respectively). Would such an asymmetry cause bottles placed on the hooks to topple the bottle dryer due to the unequal distribution of weight among the four quadrants or would the bottles overlap and therefore, make the rack not fully functional? Both effects would be testable by putting bottles on the hooks and observing the results. All commercial French bottle racks that I have seen contain an equal number of hooks in each quadrant of each tier. I am planning to alter an existing rack to match Duchamp’s original (which is probably what he did in the first place).
And what about the Bicycle Wheel on a stool? When I examined the various photos of the (alleged) second lost version in Duchamp’s studio and compared them with later readymade reproductions, I soon noted that in three different studio views, the allegedly same stool had different rungs missing (See illustrations 15A ,15B & 15C ).

Duchamp’s studio, 1917-1918, with Bicycle
Wheel on stool, 1913, gelatin silver print,
2nd reproduction (lost), (Courtesy of
anonymous private collection.)
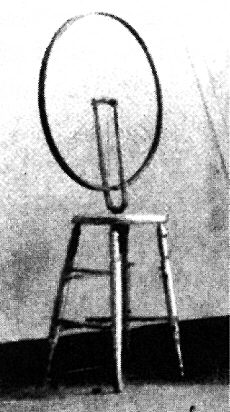
studio, 1917-1918, with Bicycle Wheel on stool,
1913, gelatin silver print, 2nd reproduction (lost),
(Courtesy of anonymous private collection.)
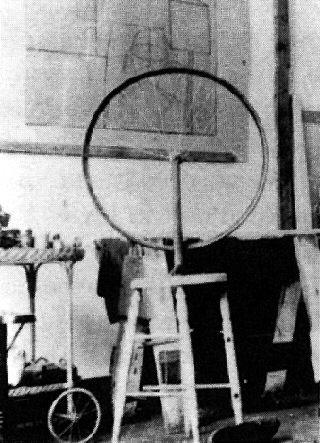
Bicycle Wheel in foreground) 1917-1918, Roche, Henri-Pierre or
Duchamp, Marcel, gelatin silver print, 3¼” x 2½,” private collection.
Rungs emerge and disappear, in whole and in part, essentially indicating that these photos represent either three different stools or doctored photographs.
Duchamp admitted that he retouched photographs. In the coat rack, this touching up is overt, although its purpose is not clear. Since we know that Duchamp doctored some photographs, shouldn’t we be skeptical about what we see (retinally) in his other photographs, on the alert for other, perhaps undeclared, photographic alterations? In the case of the Bicycle Wheel (1913), why has no one questioned the discrepancies among the three versions of what is supposed to be the original stool? How can this “original” stool be considered a readymade from a store? And how, then, can it be used for further reproductions? Moreover, how did all the alleged Bicycle Wheel on a stool “reproductions” get “reproduced” with no broken or missing rungs? Was all this a test set by Duchamp for those doing the reproductions? Or did Duchamp allow the production of complete stools in order to encourage us in our false assumption that a readymade is an unchanged everyday object-the “I can also buy it at the store” artist’s mythology?
One can also question the readymade entitled 50 cc of Paris Air (1919). This same unnamed person noted that the break at the stem where the glass hook meets the glass bulb seemed suspicious. We both questioned wheteh hooks were part of the standard design for this type of pharmacy vial, and I am presently doing research to find the answer. A second question concerns the title of 50 cc of Paris Air. Why only 50cc’s in the title, when the container apparently holds 125cc’s (Bonk, 1989, p. 202)?
Kirk Varnedoe, Director of Paintings and Sculptures at the Museum of Modern Art, told me that, for his High/Low exhibition, his researchers looked everywhere for readymades identical with Duchamp’s “lost” originals (personal communication, Fall, 1997). They were able to find only two “probable” examples of Duchamp’s Fountain urinal (1917) and his Comb (1916) (Varnedoe & Gopnick, 1991, pp. 272-278). Duchamp claimed that his “Comb” was for dogs, but the research of Varnedoe’s colleagues indicates that this strange Comb (with such small teeth) was probably only part of a larger cow grooming device. Duchamp’s original Fountain urinal is supposedly shown in three photographs: (1) two in his studio, strangely hanging from a door frame; and (2) the famous photo that Duchamp had taken by Alfred Steiglitz. Inconsistency arises again in the case of these three photographs of the urinal; the three examples do not seem to match. Moreover, whereas we observe only one set of holes in the “lost” original, the full-scale reproductions (and some later versions for the Bôite) have two sets of holes, a design that is both traditional and necessary for flushing and draining functions. I plan to do a computer analysis to try to match the two urinals in the two photographs in order to determine whether or not they represent the same form.
According to Varnedoe (personal communication, Fall, 1997), scholars have often tried to replicate Duchamp’s 3 Standard Stoppages (1913-1914) (See image below). In this piece, Duchamp claims to have taken three meter length threads, dropped them from a height of one meter, and then glued the resulting forms to blue canvas with drops of varnish. I dropped meter threads too, following Duchamp’s protocol, and never even got close to obtaining the results claimed by Duchamp. Something was very wrong. I even cut additional threads and tried to match the curves in his three threads by superimposing mine over his. The inherent elasticity of thread never allowed to exactly match the curves of his threads. Several times I came fairly close to matching my thread to his; but as soon as I tried to replicate my “experiment,” the thread would suddenly become either too long or too short, a result apparently caused by the stretching or restraining efforts of my previous attempt. It was a “crazy making” experience-neither dropping nor hand manipulation of the threads created predictable results or replication. In fact, I am not sure how Duchamp was able to obtain his original results.
As for Duchamp’s “lost” Underwood typewriter cover readymade (Traveler’s Folding Item, 1916), Nesbit and Sawelson-Gorse (1996) discovered an actual example from an Underwood company ad of this period. But again, when we compare Duchamp’s lost version with this official image, the shapes do not match. Duchamp’s typewriter cover clearly does not adhere to the slanting angles of an actual typewriter.
Finally, what about Duchamp’s Pharmacy, a supposedly readymade landscape image, with two colored dots placed within the background? When we look at various versions of the Pharmacy (1914) or read Duchamp’s own commentaries on this piece, sometimes he specifies red and yellow dots, but at other times, red and green. It all depends on which interview you read, or which version you see (see Cabanne, 1967, p. 47; Sanouillet & Peterson, 1973, p. 41; Schwarz, 1969a, p. 445). 28 Duchamp proclaimed that the ability of the unconscious to be creative was genetically inherited and could not be learned; he compares not having this “esthetic ech Duchamp proclaimed that the ability of the unconscious to be creative was genetically inherited and could not be learned; he compares not having this “esthetic echo” to being “color blind” and not being physically able to see red and green (see Clearwater, 1991, p. 52). Is his Pharmacy readymade a “non-retinal vision exercise,” where if we notice that red and green is sometimes red and yellow-and that this inconsistency is part of a larger pattern of inconsistencies in his readymades-we are led to the realization that the readymades are not merely unaltered manufactured objects? Do we pass the test by understanding that they are three- and two-dimensional non-retinal objects that can be truly perceived and understood only by the 4-D mind that questions the retinal? In the next issue of Art & Academe, 29 Part II of this paper will address the “wrong readymades” in their relation to the Large Glass and the 3 Standard Stoppages.
NOTES Part I
BIBLIOGRAPHY Part I
Adcock, C. [1984, Fall]. “Conventionalism in Henri Poincaré and Marcel Duchamp.” Art Journal, pp. 249-258.
Bonk, E. [1989]. Marcel Duchamp: The Box in a Valise. New York: Rizzoli.
Cabanne, P. [1967]. Dialogues With Marcel Duchamp. London: DaCapo Press.
Clearwater, B. [Ed.]. [1991]. West Coast Duchamp. Miami Beach, FL: Grassfield Press.
Davis, D.M. [1993]. The Nature and Power of Mathematics. Princeton, NJ: Princeton University Press.
d’Harnoncourt, A., & McShine, K. [1973]. Marcel Duchamp. New York: The Museum of Modern Art.
Diacu, F., & Holmes, P. [1996]. Celestial Encounter: The Origins of Chaos and Stability. Princeton, NJ: Princeton University Press.
Duchamp, M. [1960]. “The Bride Stripped Bare by Her Bachelors, Even.” In a typographic version of the Green Box Notes by Richard Hamilton: London: Hansjörg, Mayer, Stuttgart.
Duchamp, M. [1966]. The White Box [C. Gray, Trans.]. New York: Cordier and Ekstrom Gallery. [Original work, L’infinitif, published 1966].
Ernst, B. [1992]. Optical Illusions. New York: Taschen America Inc.
Ernst, B. [1996]. Adventures with Impossible figures. New York: Taschen America Inc.
Escher, M.D. [1986]. Escher on Escher. New York: Harry N. Abrams.
Fineman, M. [1981]. The Nature of Visual Illusions. New York: Dover.
Gervais, A. [1984]. La Raie Allité d’effets. Montreal: HMH.
Gregory, R.L. [1979]. Eye and Brain [3rd ed.]. Princeton, NJ: Princeton University Press.
Gregory, R.L. [Ed.]. [1973]. Illusion in Nature and Art. London: Duckworth.
Hahn, O. [1966, July]. “Passport No. 622553300.” Art and Artists,1[4], p. 10.
Henderson, L.D. [1983]. The Fourth Dimension and Non-Euclidean Geometry in Modern Art. Princeton, NJ: Princeton University Press.
Hulton, P. [Ed.]. [1993]. Marcel Duchamp: Work and Life. Cambridge, MA: M.I.T. Press.
Maharaj, S. [Ed.]. [1996]. “A Monster of Veracity, a Crystalline Transubstantiation: Typotranslating the Green Box.” In M. Buskirk & M. Nixon [Eds.], The Duchamp Effect [p. 68]. Cambridge, MA: M.I.T. Press.
Matisse, P. [Ed.]. [1980]. Marcel Duchamp: Notes. Paris, France: Centre National D’Art te de Culture George Pompidou.
Miller, A. [1936, August 16]. “Painter Hits Art Theory.”Los Angeles Times.
Nesbit, M. [1991]. “The Language of Industry.” In T. De Duve [Ed.], The Definitively Unfinished Marcel Duchamp [pp. 351-385]. Cambridge, MA: M.I.T. Press.
Nesbit, M. & Sawelson-Gorse, N. [1996]. “Concept of Nothing.” In M. Buskirk & M. Nixon [Eds.], The Duchamp Effect [p. 153]. Cambridge, MA: M.I.T. Press.
Penrose, R. [1973]. “In Praise of Illusions.” In R.L. Gregory [Ed.], Illusion in Nature and Art [p. 245]. London: Duckworth.
Penrose, L., & Penrose, R. [1958]. “Impossible Objects: A Special Type of Illusion.” British Journal of Psychology, 49, p. 31.
Peterson, I. [1993]. Newton’s Clock: Chaos in the Solar System. New York: W.H. Freedman.
Poincaré, H. [1908]. Science and Method. New York: Dover.
Roberts, F. [1968, December]. “I Propose to Strain the Laws of Physics.” Art News 67[8], p. 62. New York: W.H. Freedman.
Ruelle, D. [1991]. Chance and Chaos. Princeton, NJ: Princeton University Press.
Sanouillet, M. & Peterson, E. [Eds.] [1973]. Writings of Marcel Duchamp. New York: DeCapo Press.
Schwarz, A. [1969a]. The Complete Works of Marcel Duchamp. New York: Harry N. Abrams.
Schwarz, A. [1969b]. Projects and Notes for the Large Glass. New York: Harry N. Abrams.
Shearer, R.R. [1998]. The Flatland Hypothesis: A New Look at Revolutions in Art and Science. New York: Copernicus.
Shearer, R.R. [1997a, March/April]. “Coffee Mates.” The Sciences, 37, pp. 14, 15.
Shearer, R.R. [1997a, September/October]. “What’s In A Word.” [Letter Exchange with Francis Naumann]. The Sciences, 37, pp. 7, 63, 64.
Tomkins, C. [1965]. The Bride and the Bachelors. New York: Viking Press.
Varnedoe, K., & Gopnik, A. [1991]. High and Low. Exhibition Catalogue, The Museum of Modern Art. New York: Harry N. Abrams.



